Upravljanje proizvodnega sistema z zakasnitvami v proizvodnji s pomočjo Lambertovih funkcij
DOI:
https://doi.org/10.18690/analipazu.7.1-2.26-34.2017Ključne besede:
Lambertove funkcije, proizvodni sistem z zakasnitvijo, zmanjševanje proizvodnih stroškov, diferencialna enačba proizvodnega sistema z zakasnitvijo, stabilnostna mejaPovzetek
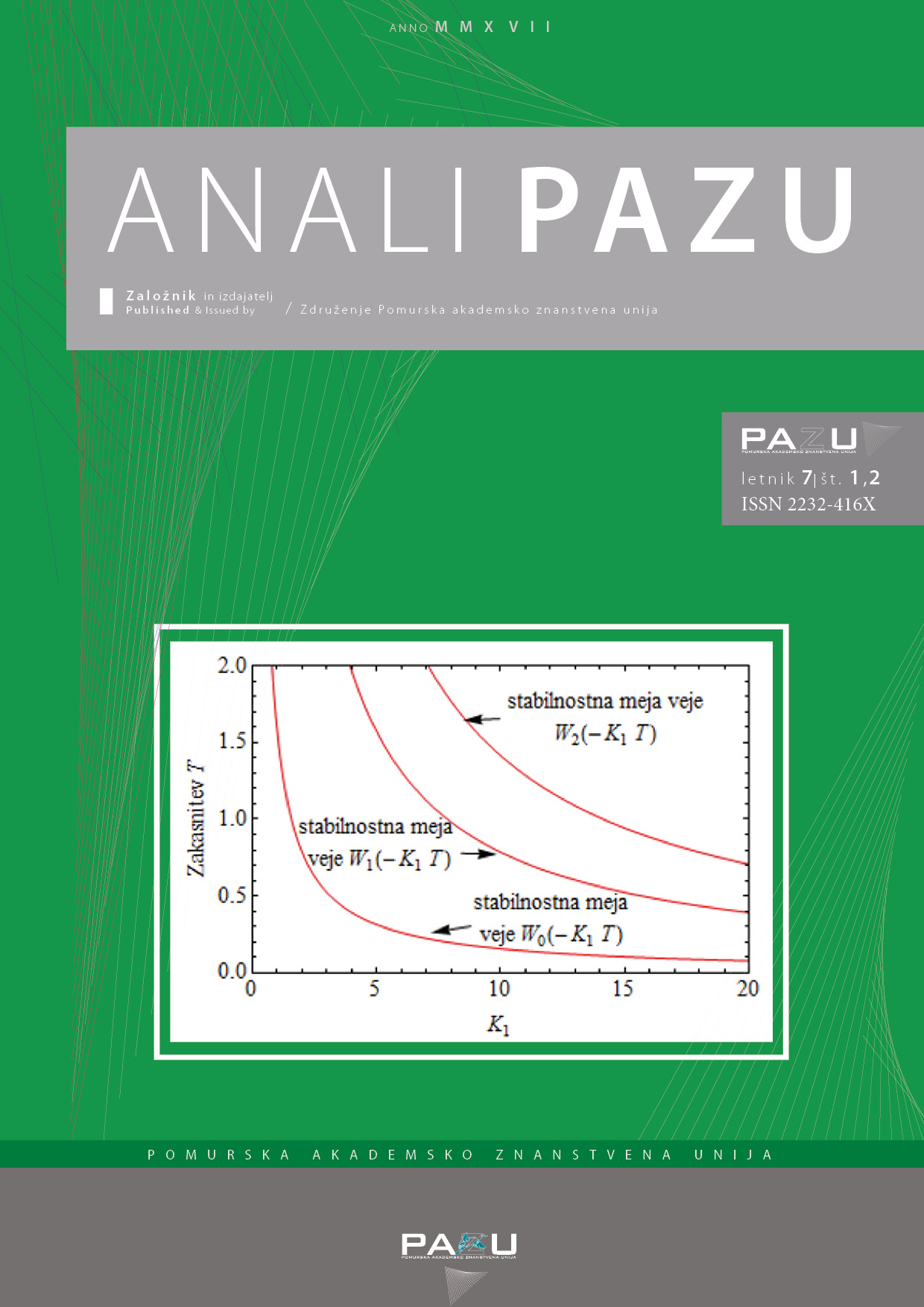
Članek obravnava upravljanje proizvodnega procesa z zakasnitvami v proizvodnji. Namen upravljanja proizvodnega sistema je optimiranje količine proizvodnje tako, da zmanjšamo proizvodne stroške v izbranem časovnem obdobju na minimum. Upravljanje je prikazano v enostavnem proizvodnem sistemu z zakasnitvami, v katerem poteka neprekinjena proizvodnja posameznega izdelka. Za doseganje optimalne proizvodnje so v prispevku uporabljene Lambertove funkcije, s katerimi omogočimo tvorbo analitičnih rešitev linearne diferencialne enačbe z zakasnitvami, ki opisuje proizvodni proces. V članku je raziskana stabilnost upravljanja proizvodnega sistema z določitvijo stabilnostne meje v analitični obliki. Pri tem je ugotovljeno, da zakasnitve proizvodnje povzročajo nihajoči potek dejanskih zalog v odvisnosti od časa, pri čemer z upravljanjem proizvodnje ta nihanja uspešno zadušimo, v kolikor se časovna zakasnitev in stopnja načrtovane proizvodnje na osnovi informacije o pogrešku regulacije nahajata v stabilnem področju. Dobljeni analitični rezultati so primerjani z numerično rešitvijo po metodi Runge-Kutta v programskem okolju Mathematica, pri čemer je ugotovljeno skoraj popolno ujemanje.